An den Kanten des Würfels und an den Bodenkacheln (nur bei Bewegung der Kamera), die in Wirklichkeit quadratisch sind, erkennt man deutlich die auftretende hyperbelartige Verzerrung.

Eine Kamera bewegt sich mit hoher Geschwindigkeit auf einen Würfel zu, wobei die Positionen von Kamera und Würfel etwas versetzt zueinander sind. Das Licht der oberen und unteren Würfelkante hat einen längeren Weg bis zur Kamera als das Licht der Würfelmitte, es benötigt also mehr Zeit. Das Ergebnis ist im Bild deutlich zu sehen: Der obere und untere Teil der Kanten des Würfels werden weiter hinten im Bild dargestellt als der mittlere Teil: Das Licht musste zu einem früheren Zeitpunkt starten, um gleichzeitig in die Kamera zu gelangen.

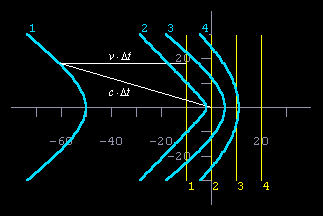
Die endliche Lichtlaufzeit führt dazu, dass Punkte, die unterschiedlich weit von der Kamera entfernt sind, zu unterschiedlichen Zeiten abgebildet werden. Punkte, die weiter von der Kamera entfernt sind, erscheinen auf dem Bild zu einem früheren Zeitpunkt als kameranahe Punkte; sie werden also im Bild weiter hinten dargestellt.

Es lässt sich zeigen, dass gerade Linien senkrecht zur Bewegungsrichtung aufgrund der Retardierung hyperbelartig verformt werden.

Die Retardierungsbedingungen lauten:

Elimination der Laufzeit aus den beiden Gleichungen führt auf eine Hyperbelgleichung.